NÚmero de oro:
Estamos en el siglo VI antes de Cristo. Pitágoras, huyendo de Polícrates, el tirano que reinaba en la isla griega de Samos, se establece en Crotona, Italia, y funda la "Hermandad Pitagórica", una escuela de filosofía y matemáticas, una especie de secta de la que él era el gran maestro.
Trataban de explicar la vida mediante números, de ahí que el principio básico de la hermandad fuera: "Todo es número". Se comunicaban mediante un símbolo secreto: la estrella de 5 puntas, que se obtiene trazando las diagonales de un pentágono regular.
Estudiándola descubrieron que, si divides en cualquier pentágono regular el valor de la diagonal entre el valor del lado, el número que obtienes es siempre el mismo, 1,61803.........................
Habían encontrado el número de oro, al que nosotros llamaremos Phi en honor al escultor Fidias, que tanto lo utilizó, y representaremos con la letra griega ø, la inicial del nombre de "Phidias" en griego.
Pero algo les desconcertó: hasta entonces, todos los números conocidos podían expresarse como un cociente entre dos números naturales, ese número no.
Era inexplicable para ellos, atentaba contra su propia concepción del mundo, así que incluso decidieron ocultarle a la sociedad que habían descubierto un nuevo tipo de números, los números irracionales
Serie de Fibonacci
Una sucesión de Fibonacci es aquella cuya ley de recurrencia es:
an = an-1 + an-2
Es decir, cada término de la sucesión se obtiene sumando los dos anteriores. Para empezar a construirla necesitamos, por tanto, dos números de partida, a1 y a2. De esta forma, a3 sería a2 + a1; a4 sería a3 + a2 y así sucesivamente.
La más conocida es la que tiene a1 = 1 y a2 = 1, cuyos términos son:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 ...
Números que son conocidos como Números de Fibonacci.
Los términos de cualquier sucesión de Fibonacci tienen la particularidad de que el cociente entre dos términos consecutivos se aproxima al Número de Oro (1.6180339887499...), es decir, el límite de los cocientes an+1/an tiende al Número de Oro cuando n tiende a infinito.
Además, las series de Fibonacci cumplen otras curiosas propiedades, como por ejemplo, que la suma de n términos es igual al término n+2 menos uno:
a1 + a2 + a3 + a4 + ..... + an-1 + an = an+2 - 1
Otra forma de poder deducir esta serie es a través de números nominales. En la cual se el primer número es 1, el cual en nominal se traduce a 1/1.
Ahora para poder deducir el próximo número de la serie, se suman en numerador y denominador y el resultado de esta será el denominador del siguiente, y el denominador anterior se pasa como el numerador siguiente.
Así que por resultado el número siguiente sería: ½ . Y se continúa igual para sacar los próximos números, al llegar a 21/34 es cuando se llega al mismo número de oro.
Sección Áurea
En 1497, un fraile italiano llamado Lucca Pacioli escribió un libro donde se reveló, por fin, el secreto de la belleza. Se titula De divina Proportione, y su tema central es lo que los escolares de nuestros días conocen como "regla de tres". Pacioli se inspiraba en las ideas de Piero della Francesca, un hombre que hoy conocemos a través de su obra pictórica, pero que en su tiempo era más conocido por ser el autor de De Abaco, un manual de matemática para comerciantes.
La regla de tres era una herramienta básica para los comerciantes del Quattrocento: servía para determinar las proporciones de capital, tierras, volumen de grano o cualquier otra clase de bienes que le correspondía a cada socio, heredero o copropietario ante un total determinado. Se la conocía entonces como regla de oro o llave del comerciante.
Una regla de tres famosa es la llamada Escala Armónica Pitagórica, que al modo renacentista se expresa: 6 8 9 12
Algunos arquitectos relacionaron la escala armónica pitagórica, utilizada para representar una escala musical, con el diseño visual modular o proporcional. Andrea Palladio dejó asentada una falacia de diseño según la cual los espacios pueden ser diseñados "musicalmente" de acuerdo con esta escala: como el intervalo entre 6 y 12 es de una octava, entre 6 y 9 y entre 8 y 12 es de una quinta, entre 6 y 8 y entre 9 y 12 de cuarta y entre 8 y 9 de un tono, si se organizaban las dimensiones de las habitaciones de un edificio siguiendo esta serie, entonces se estaría produciendo una armonía espacial de la misma clase que la que relaciona las notas musicales. La regla Áurea parecía una fórmula perfecta que relacionaba las artes de la música, la pintura y la arquitectura. Y además mantenía las buenas relaciones comerciales.
Cuando Lucca Pacioli escribió La Divina Proporción, lo que hizo fue tomar otro tipo de regla de tres, que, partiendo de una unidad arbitraria permitía la construcción de proporcionalidades tanto de múltiplos como de submúltiplos (intervalos mayores y menores). Los aficionados (en particular los fotógrafos, grandes entusiastas) conocen esta relación como sección áurea. Su expresión matemática es
a:b=b:a+b
Vitruvio ideó un sistema de cálculo matemático de la división pictórica, para seccionar los espacios en partes iguales y así conseguir una mejor composición. Se basa en el principio general de contemplar un espacio rectangular dividido, a grandes rasgos, en terceras partes, tanto vertical como horizontalmente. O, explicado de otra forma, bisecando un cuadro y usando la diagonal de una de sus mitades como radio para ampliar las dimensiones del cuadrado hasta convertirlo en "rectángulo áureo". Se llega a la proporción a: b = c: a. Al situar los elementos primordiales de diseño en una de estas líneas, se cobra conciencia del equilibrio creado entre estos elementos y el resto del diseño.
Un rectángulo especial es el llamado rectángulo áureo. Se trata de un rectángulo armonioso en sus dimensiones.
Dibujamos un cuadrado y marcamos el punto medio de uno de sus lados. Lo unimos con uno de los vértices del lado opuesto y llevamos esa distancia sobre el lado inicial, de esta manera obtenemos el lado mayor del rectángulo.
Si el lado del cuadrado vale 2 unidades, es claro que el lado mayor del rectángulo vale 1+ 5 por lo que la proporción entre los dos lados es:
(1+ 5 ) /2
A este número se le llama número de oro, se representa por el símbolo Ø y su valor es 1,61803..., lo obtuvieron los griegos al hallar la relación entre la diagonal de un pentágono y el lado. El nombre de "número de oro" se debe a Leonardo da Vinci.
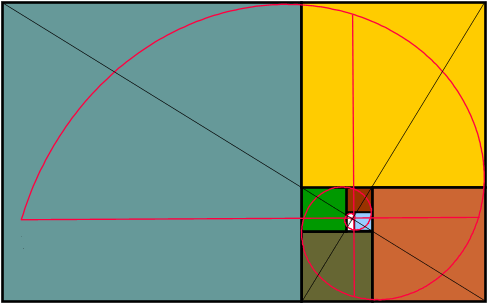
Una manera práctica de dibujar una espiral es mediante la construcción rectangular en las espirales de cuadrados; se trata de dibujar el cuadrante de un círculo en cada nuevo cuadrado que se añada.
La divina proporción
Durante los últimos siglos, creció el mito de que los antiguos griegos estaban sujetos a una proporción numérica específica, esencial para sus ideales de belleza y geometría. Dicha proporción es conocida con los nombres de razón áurea ó divina proporción. Aunque recientes investigaciones revelan que no hay ninguna prueba que conecte esta proporción con la estética griega, esta sigue manteniendo un cierto atractivo como modelo de belleza.
Matemáticamente nace de plantear la siguiente proporcionalidad entre dos segmentos y que dice así: "Buscar dos segmentos tales que el cociente entre el segmento mayor y el menor sea igual al cociente que resulta entre la suma de los dos segmentos y el mayor"
Sean los segmentos:
A: el mayor y B el menor, entones planteando la ecuación es:
A/B =(A+B)/A
Ahora por mencionar poco, todos estos datos terminan en lo mismo, en su aplicación, numerología, y demás, dejando fuera de dudas en que en verdad la naturaleza misma es sorprendente y más aun cuando nosotros nos introducimos un poco más a investigarla y dejarnos sorprender como aprender de ella.